Sudoku: Hidden Candidates Reduction Method Clarified

In Sudoku ‘hidden’ candidates may be present in pairs, triples or quads. The candidates are ‘hidden’ if they are not alone but ‘hidden’ among other candidates in the squares. If ‘hidden’ candidates are present, those numbers must necessarily be in the squares where they are – they are linked to those squares. Therefore, any other candidates present in the squares with ‘hidden’ candidates can be removed from those squares. In the squares with ‘hidden’ candidates we do not yet know where each of the numbers should be placed, only that they collectively should be in those squares. Later in the solving process the unique position of each number will become clear. Now we will go through he method for pairs, triples and quads and give some examples.

Sudoku Hidden Pair

If the same pair of candidates are ‘hidden’ among other candidates in just two squares within a group (row, column or block), then these candidates make up a ‘hidden’ pair. Neither of the candidates must be present in any other square within the group. Thus two numbers are limited and therefore linked to those two squares. Therefore, other candidate numbers can be removed from those two squares within the group.

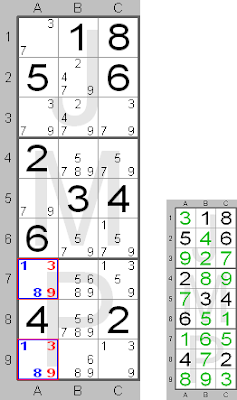This board shows a 'hidden' pair (1 and 8, shown in blue) in column A in squares A7 and A9. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 1 and 8 are linked to those squares. Therefore the other candidate numbers, which are present in those squares, can be removed. The candidate numbers, which can be removed (6 and 9), are shown in red.
In the small picture you can see the final solution for this part of the board. In column A number 1 should be in square A7 and number 8 in square A9.

Sudoku Hidden Triples

If the same three candidates are ‘hidden’ among other candidates in just three squares within a group (row, column or block), then these candidates make up ‘hidden’ triples. None of the candidates must be present in any other square within the group. Thus the three candidate numbers are limited to and therefore linked to those three squares. Therefore, other candidate numbers can be removed from those three squares within the group.



This board shows 'hidden' triples (1, 2 and 7, shown in blue) in row 3 in squares A3, C3 and F3. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 1, 2 and 7 are linked to those squares. Therefore other candidate numbers being present in those squares can be removed. The candidate numbers, which can be removed (4 in A3, 6 in C3 and 6 and 9 in F3), are shown in red.
In the small picture you can see the final solution for this part of the board. In row 3 number 1 should be in square A3, number 2 in square C3 and number 7 in square F3.

Sudoku Hidden Quads

If the same four of candidates are ‘hidden’ among other candidates in just four squares within a group (row, column or block), then these candidates make up ‘hidden’ quads. None of the candidates must be present in any other square within the group. The three numbers are limited to and therefore linked to those four squares. Therefore, other candidate numbers can be removed from those four squares within the group.

This board shows 'hidden' quads (2, 3, 4 and 6, shown in blue) in block P in squares B2, C1, C2 and C3. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 2, 3, 4 and 6 are linked to those squares. Therefore other candidate numbers being present in those squares can be removed. The candidate numbers, which can be removed (5 from C1, 7 from B2, C2 and C3 and 8 from B2, C1, C2 and C3), are shown in red.
In the small picture you can see the final solution for this part of the board. In block P number 3 should be in square B2, number 6 in square C1, number 4 in square C2 and number 2 in square C3.

This method of finding ‘hidden’ candidates in a Sudoku puzzle can be used repeatedly for candidate reduction. Thereby, more single candidates may appear making it easier to solve the Sudoku puzzle. In the next post we will go through even more elaborate methods of candidate reduction.