Here is a fine Sudoku Program to assist you throughout the solving process. Simple and easy.
This video shows you how to solve a Sudoku Puzzle. It is easy to follow.
Sunday, December 27, 2009
Simple Tips On Solving A Sudoku Puzzle
Here is a good Sudoku Program, which helps and assists you in solving any Sudoku puzzle.
This video really gives some good hints on how to solve Sudoku puzzles.
This video really gives some good hints on how to solve Sudoku puzzles.
Monday, November 9, 2009
Sudoku Instructions: A Program Showing How To Solve Sudoku Puzzles
The graphics used in the previous posts in this blog have been made using the Sudoku Instructions program, which we have developed. You can obtain it from Sudoku Instructions website. The program is very user-friendly. It is designed to assist you in solving any sudoku puzzle by guiding you all the way through the solving process.
We wish you the best of luck in your Sudoku playing! Best regards, ERVICH
We wish you the best of luck in your Sudoku playing! Best regards, ERVICH
Saturday, November 7, 2009
Sudoku: ‘X-Wing’, ‘Swordfish’ and ‘Jellyfish’ Clarified
These more difficult methods for candidate reduction in Sudoku are based on the relationship of a candidate number with both rows and columns. The X-wing is applied for two rows and two columns, the Swordfish for three rows and three columns and the Jellyfish for four rows and four columns. For an X-wing to be present the same candidate number must be present in all four squares where the rows and columns cross each other. For swordfish and jellyfish the candidate number in question need not be present in all the squares where the columns and rows cross each other. The rather odd names of these methods may relate very faintly to the outline of the involved squares with the candidate number in question. We will understand more of these difficult methods if we start with the simplest, namely the X-wing.
Sudoku X-wing – Rows/Columns
If the same candidate number within two rows is limited to the same two columns, then that number must necessarily be in two of the four ‘crossing-squares’ where the rows and columns cross each other. Since that number can only be once in each of the two columns, the candidate number can be removed from the two columns outside the two rows. This method, which focuses on two times two squares, is called an X-wing. We do not know in which two of the four ‘crossing-squares’ the number should be placed. Either the number should be placed as indicated by the \ part of the X or as indicated by the / part of the X. The exact place would become clear later in the solving process.
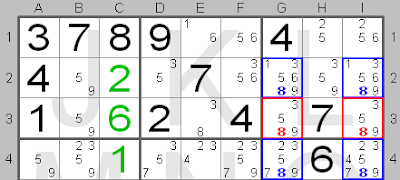
This board shows an 'X-wing' for candidate number 8 (shown in blue), which forms an X-wing in squares G2, G4, I2 and I4, because in rows 2 and 4 candidate number 8 is only present in columns G and I. So, in these columns candidate number 8 must be in rows 2 and 4. Therefore in these columns candidate number 8 can be removed from the other rows, here row 3 in squares G3 and I3 (shown in red).
In the small picture you can see the final solution for this part of the board. In row 2 number 8 should be in square G2 and in row 4 number 8 should be in square I4.
Sudoku X-wing – Columns/Rows
If the same candidate number within two columns is limited to the same two rows, then that number must necessarily be in two of the four ‘crossing-squares’ (the X-wing) where the columns and rows cross each other. Since that number can only be once in each of the two rows, the candidate number can be removed from the two rows outside the two columns. We do not know in which two of the four ‘crossing-squares’ the number should be placed. Either the number should be placed as indicated by the \ part of the X or as indicated by the / part of the X. The exact place would become clear later in the solving process.
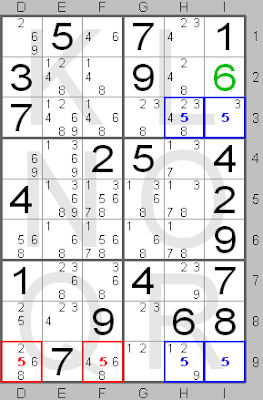
This board shows an 'X-wing' for candidate number 5 (shown in blue), which forms an X-wing in squares H3, I3, H9 and I9, because in columns H and I candidate number 5 is only present in rows 3 and 9. So, in these rows candidate number 5 must be in columns H and I. Therefore in these rows candidate number 5 can be removed from the other columns, here columns D and F in squares D9 and F9 (shown in red).
In the small picture you can see the final solution for this part of the board. In column H number 5 should be in square H3 and in column I number 5 should be in square I9.
Sudoku Swordfish - Rows/Columns
If the same candidate number within three rows is limited to the same three columns, then that number must necessarily be in three of the ‘crossing-squares’ (the ‘swordfish’) where the rows and columns cross each other. Since that number can only be once in each of the three columns, the candidate number can be removed from the three columns outside the three rows. We do not know in which three of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
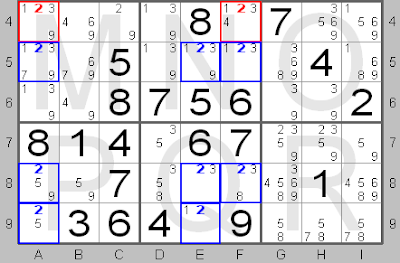
This board shows a 'Swordfish' for candidate number 2 (shown in blue), which forms a swordfish in squares A5, A8, A9, E5, E8, E9, F5 and F8, because in rows 5, 8 and 9 candidate number 2 is only present in columns A, E and F. So, in these columns candidate number 2 must be in rows 5, 8 and 9. Therefore in these columns candidate number 2 can be removed from the other rows, here row 4 in squares A4 and F4 (shown in red).
In the small picture you can see the final solution for this part of the board. Number 2 should in square A9 in column A, in square E8 in column E and in square F5 in column F.
Sudoku Swordfish – Columns/Rows
If the same candidate number within three columns is limited to the same three rows, then that number must necessarily be in three of the ‘crossing-squares’ (the ‘swordfish’) where the columns and rows cross each other. Since that number can only be once in each of the three rows, the candidate number can be removed from the three rows outside the three columns. We do not know in which three of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
This board shows a 'Swordfish' for candidate number 8 (shown in blue), which forms a swordfish in squares A2, A4, C2, C5, E4 and E5, because in columns A, C and E candidate number 8 is only present in rows 2, 4 and 5. So, in these rows candidate number 8 must be in columns A, C and E. Therefore in these rows candidate number 8 can be removed from the other columns, here column F in squares F4 and F5 (shown in red).
In the small picture you can see the final solution for this part of the board. Number 8 should in square A2 in column A, in square C5 in column C and in square E4 in column E.
Sudoku Jellyfish - Rows/Columns
If the same candidate number within four rows is limited to the same four columns, then that number must necessarily be in four of the ‘crossing-squares’ (the ‘jellyfish’) where the rows and columns cross each other. Since that number can only be once in each of the four columns, the candidate number can be removed from the four columns outside the four rows. We do not know in which four of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
This board shows a 'Jellyfish' for candidate number 2 (shown in blue), which forms a jellyfish in squares D3, D5, E2, E3, E5, G2, G3, G4, H2, H4 and H5, because in rows 2, 3, 4 and 5 candidate number 2 is only present in columns D, E, G and H. So, in these columns candidate number 2 must be in rows 2, 3, 4 and 5. Therefore in these columns candidate number 2 can be removed from the other rows, here row 1 in squares D1, E1 and H1 (shown in red).
In the small picture you can see the final solution for this part of the board. Number 2 should in square D5 in column D, in square E2 in column E, in square G3 in column G and in square H4 in column H.
Sudoku Jellyfish – Columns/Rows
If the same candidate number within four columns is limited to the same four rows, then that number must necessarily be in four of the ‘crossing-squares’ (the ‘jellyfish’) where the columns and rows cross each other. Since that number can only be once in each of the four rows, the candidate number can be removed from the four rows outside the four columns. We do not know in which four of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
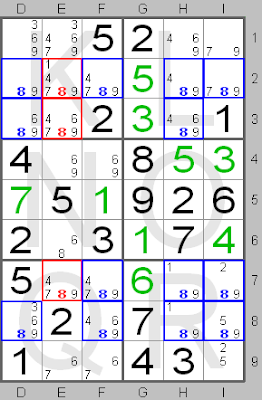
This board shows a 'Jellyfish' for candidate number 8 (shown in blue), which forms a jellyfish in squares D2, D3, D8, F2, F7, F8, H2, H3, H7, H8, I2, I7 and I8, because in columns D, F, H, and I candidate number 8 is only present in rows 2, 3, 7 and 8. So, in these rows candidate number 8 must be in columns D, F, H and I. Therefore in these rows candidate number 8 can be removed from the other columns, here column E in squares E2, E3 and E7 (shown in red).
In the small picture you can see the final solution for this part of the board. Number 8 should in square D3 in column D, in square F8 in column F, in square H7 in column H and in square I2 in column I.
As you have seen these methods are not very easy to use. They need access to the candidate table and even then it may be difficult to spot a jellyfish or a swordfish. The X-wing, which is the simplest of these methods, may also be rather difficult to spot. To apply these methods in practice you would have great help of a user-friendly Sudoku program.
Sudoku X-wing – Rows/Columns
If the same candidate number within two rows is limited to the same two columns, then that number must necessarily be in two of the four ‘crossing-squares’ where the rows and columns cross each other. Since that number can only be once in each of the two columns, the candidate number can be removed from the two columns outside the two rows. This method, which focuses on two times two squares, is called an X-wing. We do not know in which two of the four ‘crossing-squares’ the number should be placed. Either the number should be placed as indicated by the \ part of the X or as indicated by the / part of the X. The exact place would become clear later in the solving process.
This board shows an 'X-wing' for candidate number 8 (shown in blue), which forms an X-wing in squares G2, G4, I2 and I4, because in rows 2 and 4 candidate number 8 is only present in columns G and I. So, in these columns candidate number 8 must be in rows 2 and 4. Therefore in these columns candidate number 8 can be removed from the other rows, here row 3 in squares G3 and I3 (shown in red).
In the small picture you can see the final solution for this part of the board. In row 2 number 8 should be in square G2 and in row 4 number 8 should be in square I4. Sudoku X-wing – Columns/Rows
If the same candidate number within two columns is limited to the same two rows, then that number must necessarily be in two of the four ‘crossing-squares’ (the X-wing) where the columns and rows cross each other. Since that number can only be once in each of the two rows, the candidate number can be removed from the two rows outside the two columns. We do not know in which two of the four ‘crossing-squares’ the number should be placed. Either the number should be placed as indicated by the \ part of the X or as indicated by the / part of the X. The exact place would become clear later in the solving process.
This board shows an 'X-wing' for candidate number 5 (shown in blue), which forms an X-wing in squares H3, I3, H9 and I9, because in columns H and I candidate number 5 is only present in rows 3 and 9. So, in these rows candidate number 5 must be in columns H and I. Therefore in these rows candidate number 5 can be removed from the other columns, here columns D and F in squares D9 and F9 (shown in red).In the small picture you can see the final solution for this part of the board. In column H number 5 should be in square H3 and in column I number 5 should be in square I9.
Sudoku Swordfish - Rows/Columns
If the same candidate number within three rows is limited to the same three columns, then that number must necessarily be in three of the ‘crossing-squares’ (the ‘swordfish’) where the rows and columns cross each other. Since that number can only be once in each of the three columns, the candidate number can be removed from the three columns outside the three rows. We do not know in which three of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
This board shows a 'Swordfish' for candidate number 2 (shown in blue), which forms a swordfish in squares A5, A8, A9, E5, E8, E9, F5 and F8, because in rows 5, 8 and 9 candidate number 2 is only present in columns A, E and F. So, in these columns candidate number 2 must be in rows 5, 8 and 9. Therefore in these columns candidate number 2 can be removed from the other rows, here row 4 in squares A4 and F4 (shown in red).
In the small picture you can see the final solution for this part of the board. Number 2 should in square A9 in column A, in square E8 in column E and in square F5 in column F.
Sudoku Swordfish – Columns/Rows
If the same candidate number within three columns is limited to the same three rows, then that number must necessarily be in three of the ‘crossing-squares’ (the ‘swordfish’) where the columns and rows cross each other. Since that number can only be once in each of the three rows, the candidate number can be removed from the three rows outside the three columns. We do not know in which three of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
This board shows a 'Swordfish' for candidate number 8 (shown in blue), which forms a swordfish in squares A2, A4, C2, C5, E4 and E5, because in columns A, C and E candidate number 8 is only present in rows 2, 4 and 5. So, in these rows candidate number 8 must be in columns A, C and E. Therefore in these rows candidate number 8 can be removed from the other columns, here column F in squares F4 and F5 (shown in red).
In the small picture you can see the final solution for this part of the board. Number 8 should in square A2 in column A, in square C5 in column C and in square E4 in column E.
Sudoku Jellyfish - Rows/Columns
If the same candidate number within four rows is limited to the same four columns, then that number must necessarily be in four of the ‘crossing-squares’ (the ‘jellyfish’) where the rows and columns cross each other. Since that number can only be once in each of the four columns, the candidate number can be removed from the four columns outside the four rows. We do not know in which four of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
This board shows a 'Jellyfish' for candidate number 2 (shown in blue), which forms a jellyfish in squares D3, D5, E2, E3, E5, G2, G3, G4, H2, H4 and H5, because in rows 2, 3, 4 and 5 candidate number 2 is only present in columns D, E, G and H. So, in these columns candidate number 2 must be in rows 2, 3, 4 and 5. Therefore in these columns candidate number 2 can be removed from the other rows, here row 1 in squares D1, E1 and H1 (shown in red). 
In the small picture you can see the final solution for this part of the board. Number 2 should in square D5 in column D, in square E2 in column E, in square G3 in column G and in square H4 in column H.Sudoku Jellyfish – Columns/Rows
If the same candidate number within four columns is limited to the same four rows, then that number must necessarily be in four of the ‘crossing-squares’ (the ‘jellyfish’) where the columns and rows cross each other. Since that number can only be once in each of the four rows, the candidate number can be removed from the four rows outside the four columns. We do not know in which four of the ‘crossing-squares’ the number should be placed, only that it cannot be in the same row or column. Their precise position would become clear later in the solving process.
This board shows a 'Jellyfish' for candidate number 8 (shown in blue), which forms a jellyfish in squares D2, D3, D8, F2, F7, F8, H2, H3, H7, H8, I2, I7 and I8, because in columns D, F, H, and I candidate number 8 is only present in rows 2, 3, 7 and 8. So, in these rows candidate number 8 must be in columns D, F, H and I. Therefore in these rows candidate number 8 can be removed from the other columns, here column E in squares E2, E3 and E7 (shown in red).In the small picture you can see the final solution for this part of the board. Number 8 should in square D3 in column D, in square F8 in column F, in square H7 in column H and in square I2 in column I.
As you have seen these methods are not very easy to use. They need access to the candidate table and even then it may be difficult to spot a jellyfish or a swordfish. The X-wing, which is the simplest of these methods, may also be rather difficult to spot. To apply these methods in practice you would have great help of a user-friendly Sudoku program.
Thursday, November 5, 2009
Sudoku: Hidden Candidates Reduction Method Clarified
In Sudoku ‘hidden’ candidates may be present in pairs, triples or quads. The candidates are ‘hidden’ if they are not alone but ‘hidden’ among other candidates in the squares. If ‘hidden’ candidates are present, those numbers must necessarily be in the squares where they are – they are linked to those squares. Therefore, any other candidates present in the squares with ‘hidden’ candidates can be removed from those squares. In the squares with ‘hidden’ candidates we do not yet know where each of the numbers should be placed, only that they collectively should be in those squares. Later in the solving process the unique position of each number will become clear. Now we will go through he method for pairs, triples and quads and give some examples.
Sudoku Hidden Pair
If the same pair of candidates are ‘hidden’ among other candidates in just two squares within a group (row, column or block), then these candidates make up a ‘hidden’ pair. Neither of the candidates must be present in any other square within the group. Thus two numbers are limited and therefore linked to those two squares. Therefore, other candidate numbers can be removed from those two squares within the group.
This board shows a 'hidden' pair (1 and 8, shown in blue) in column A in squares A7 and A9. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 1 and 8 are linked to those squares. Therefore the other candidate numbers, which are present in those squares, can be removed. The candidate numbers, which can be removed (6 and 9), are shown in red.
In the small picture you can see the final solution for this part of the board. In column A number 1 should be in square A7 and number 8 in square A9.
Sudoku Hidden Triples
If the same three candidates are ‘hidden’ among other candidates in just three squares within a group (row, column or block), then these candidates make up ‘hidden’ triples. None of the candidates must be present in any other square within the group. Thus the three candidate numbers are limited to and therefore linked to those three squares. Therefore, other candidate numbers can be removed from those three squares within the group.
This board shows 'hidden' triples (1, 2 and 7, shown in blue) in row 3 in squares A3, C3 and F3. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 1, 2 and 7 are linked to those squares. Therefore other candidate numbers being present in those squares can be removed. The candidate numbers, which can be removed (4 in A3, 6 in C3 and 6 and 9 in F3), are shown in red.
In the small picture you can see the final solution for this part of the board. In row 3 number 1 should be in square A3, number 2 in square C3 and number 7 in square F3.
Sudoku Hidden Quads
If the same four of candidates are ‘hidden’ among other candidates in just four squares within a group (row, column or block), then these candidates make up ‘hidden’ quads. None of the candidates must be present in any other square within the group. The three numbers are limited to and therefore linked to those four squares. Therefore, other candidate numbers can be removed from those four squares within the group.
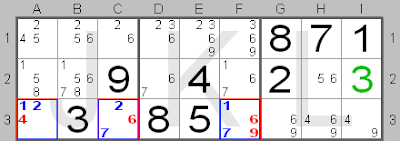
This board shows 'hidden' quads (2, 3, 4 and 6, shown in blue) in block P in squares B2, C1, C2 and C3. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 2, 3, 4 and 6 are linked to those squares. Therefore other candidate numbers being present in those squares can be removed. The candidate numbers, which can be removed (5 from C1, 7 from B2, C2 and C3 and 8 from B2, C1, C2 and C3), are shown in red.
In the small picture you can see the final solution for this part of the board. In block P number 3 should be in square B2, number 6 in square C1, number 4 in square C2 and number 2 in square C3.
This method of finding ‘hidden’ candidates in a Sudoku puzzle can be used repeatedly for candidate reduction. Thereby, more single candidates may appear making it easier to solve the Sudoku puzzle. In the next post we will go through even more elaborate methods of candidate reduction.
Sudoku Hidden Pair
If the same pair of candidates are ‘hidden’ among other candidates in just two squares within a group (row, column or block), then these candidates make up a ‘hidden’ pair. Neither of the candidates must be present in any other square within the group. Thus two numbers are limited and therefore linked to those two squares. Therefore, other candidate numbers can be removed from those two squares within the group.
This board shows a 'hidden' pair (1 and 8, shown in blue) in column A in squares A7 and A9. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 1 and 8 are linked to those squares. Therefore the other candidate numbers, which are present in those squares, can be removed. The candidate numbers, which can be removed (6 and 9), are shown in red. In the small picture you can see the final solution for this part of the board. In column A number 1 should be in square A7 and number 8 in square A9.
Sudoku Hidden Triples
If the same three candidates are ‘hidden’ among other candidates in just three squares within a group (row, column or block), then these candidates make up ‘hidden’ triples. None of the candidates must be present in any other square within the group. Thus the three candidate numbers are limited to and therefore linked to those three squares. Therefore, other candidate numbers can be removed from those three squares within the group.
This board shows 'hidden' triples (1, 2 and 7, shown in blue) in row 3 in squares A3, C3 and F3. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 1, 2 and 7 are linked to those squares. Therefore other candidate numbers being present in those squares can be removed. The candidate numbers, which can be removed (4 in A3, 6 in C3 and 6 and 9 in F3), are shown in red.
In the small picture you can see the final solution for this part of the board. In row 3 number 1 should be in square A3, number 2 in square C3 and number 7 in square F3. Sudoku Hidden Quads
If the same four of candidates are ‘hidden’ among other candidates in just four squares within a group (row, column or block), then these candidates make up ‘hidden’ quads. None of the candidates must be present in any other square within the group. The three numbers are limited to and therefore linked to those four squares. Therefore, other candidate numbers can be removed from those four squares within the group.
This board shows 'hidden' quads (2, 3, 4 and 6, shown in blue) in block P in squares B2, C1, C2 and C3. These candidates are 'hidden' because other candidates are also present in those squares. The numbers 2, 3, 4 and 6 are linked to those squares. Therefore other candidate numbers being present in those squares can be removed. The candidate numbers, which can be removed (5 from C1, 7 from B2, C2 and C3 and 8 from B2, C1, C2 and C3), are shown in red. In the small picture you can see the final solution for this part of the board. In block P number 3 should be in square B2, number 6 in square C1, number 4 in square C2 and number 2 in square C3.
This method of finding ‘hidden’ candidates in a Sudoku puzzle can be used repeatedly for candidate reduction. Thereby, more single candidates may appear making it easier to solve the Sudoku puzzle. In the next post we will go through even more elaborate methods of candidate reduction.
Thursday, October 29, 2009
Sudoku: Naked Candidates Reduction Method Clarified
In Sudoku ‘naked’ candidates may be present in pairs, triples or quads. The candidates are ‘naked’ if they are alone, i.e. not ‘hidden’ among other candidates in the squares. If ‘naked’ candidates are present those numbers must necessarily be in those squares. Therefore, those candidates can be removed the other squares within the group. In the squares with ‘naked’ candidates we do not yet know where each of the numbers should be placed, only that they collectively should be in those squares. Later in the solving process the unique position of each number will become clear. Let us go through the method for pairs, triples and quads and give some examples.
Sudoku Naked Pairs
If two squares in a group (row, column or block) have the same pair of candidate numbers and only these, then these candidates make up a ‘naked’ pair. The two numbers are linked to those two squares. Therefore, those candidate numbers can be removed from the other squares within the group.
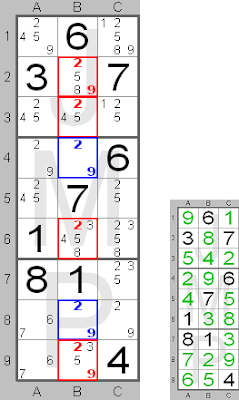This board shows a 'naked' pair (2 and 9, shown in blue) in column B in squares B4 and B8. These candidates are 'naked' because no other candidates are present in those squares. The numbers are therefore linked to those squares. The candidates, which can be removed from the other squares (2 from B2, B3, B6 and B9 and 9 from B2 and B9), are shown in red.
In the small picture you can see the final solution for this part of the board. In column B number 9 should be in square B4 and number 2 in square B8.
Sudoku Naked Triples
If in three squares within a group the candidates are limited to three numbers, those candidates make up ‘naked’ triples. All three candidate numbers need not be present in all three squares, but those numbers are linked to the three squares. Therefore those three candidate numbers can be removed from the other squares within the group.
This board shows 'naked' triples (3, 4, and 6, shown in blue) in block P in squares A8, B8 and C8. These candidates are 'naked' because no other candidates are present in those squares. The numbers are therefore linked to those squares. The candidates, which can be removed from the other squares (3, 4 og 6 from square A7, 3 and 6 from square B7, 4 and 6 from square C7 and 3, 4 and 6 from square A9), are shown in red.
In the small picture you can see the final solution for this part of the board. In block P number 6 should be in square A8, number 3 in square B8 and 4 in square C8.
Sudoku Naked Quads
If in four squares within a group the candidates are limited to four numbers those candidates make up ‘naked’ quads. All four candidate numbers need not be present in all four squares, but those numbers are linked to the four squares. Therefore those four candidate numbers can be removed from the other squares within the group.
This board shows 'naked' quads (2, 5, 7 and 9, shown in blue) in row 2 in squares D2, E2, F2 and H2. These candidates are called 'naked' because no other candidates are present in those squares. The candidates, which can be removed from the other squares (5 and 9 from squares A2 and G2), are shown in red.
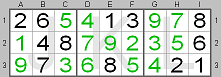In the small picture you can see the final solution for this part of the board. In row 2 number 7 should be in square D2, number 9 in square E2, number 2 in square F2 and number 5 in square H2.
This method of finding ‘naked’ candidates in Sudoku can be used repeatedly for candidate reduction. Thereby the solution of the Sudoku puzzle may be easier to find. Shortly we will go through other effective methods of candidate reduction.
Sudoku Naked Pairs
If two squares in a group (row, column or block) have the same pair of candidate numbers and only these, then these candidates make up a ‘naked’ pair. The two numbers are linked to those two squares. Therefore, those candidate numbers can be removed from the other squares within the group.
This board shows a 'naked' pair (2 and 9, shown in blue) in column B in squares B4 and B8. These candidates are 'naked' because no other candidates are present in those squares. The numbers are therefore linked to those squares. The candidates, which can be removed from the other squares (2 from B2, B3, B6 and B9 and 9 from B2 and B9), are shown in red. In the small picture you can see the final solution for this part of the board. In column B number 9 should be in square B4 and number 2 in square B8.
Sudoku Naked Triples
If in three squares within a group the candidates are limited to three numbers, those candidates make up ‘naked’ triples. All three candidate numbers need not be present in all three squares, but those numbers are linked to the three squares. Therefore those three candidate numbers can be removed from the other squares within the group.
This board shows 'naked' triples (3, 4, and 6, shown in blue) in block P in squares A8, B8 and C8. These candidates are 'naked' because no other candidates are present in those squares. The numbers are therefore linked to those squares. The candidates, which can be removed from the other squares (3, 4 og 6 from square A7, 3 and 6 from square B7, 4 and 6 from square C7 and 3, 4 and 6 from square A9), are shown in red. In the small picture you can see the final solution for this part of the board. In block P number 6 should be in square A8, number 3 in square B8 and 4 in square C8.
Sudoku Naked Quads
If in four squares within a group the candidates are limited to four numbers those candidates make up ‘naked’ quads. All four candidate numbers need not be present in all four squares, but those numbers are linked to the four squares. Therefore those four candidate numbers can be removed from the other squares within the group.
This board shows 'naked' quads (2, 5, 7 and 9, shown in blue) in row 2 in squares D2, E2, F2 and H2. These candidates are called 'naked' because no other candidates are present in those squares. The candidates, which can be removed from the other squares (5 and 9 from squares A2 and G2), are shown in red. 
In the small picture you can see the final solution for this part of the board. In row 2 number 7 should be in square D2, number 9 in square E2, number 2 in square F2 and number 5 in square H2. This method of finding ‘naked’ candidates in Sudoku can be used repeatedly for candidate reduction. Thereby the solution of the Sudoku puzzle may be easier to find. Shortly we will go through other effective methods of candidate reduction.
Wednesday, October 28, 2009
Sudoku: ‘Locked’ Candidate Reduction Method Clarified
To solve a sudoku puzzle you need to fill each empty square with one of the numbers 1 to 9. In some squares there may more than one candidate number, and it may be difficult to decide which of these candidate numbers would be the correct one. The number of candidates needs to be reduced. You need to perform a 'candidate reduction’ in the sudoku puzzle. So, you should try to locate candidates, which may safely be removed from the squares. There are various methods for doing just that. A relatively easy method is to locate a ‘locked’ candidate in the sudoku puzzle. It works like this:
Sudoku Locked Candidate: Row - Block
If in a row a candidate number is confined to a single block, it is 'locked' inside the block. Since the block can only have this number once, that candidate number can be removed from the other rows within that block.
Here you can see that within row 3 candidate number 7 only occurs inside block K (blue numbers in squares E3 and F3). So, within block K number 7 is ‘locked’ in row 3. Therefore candidate number 7 can be deleted in other rows within block K, i.e. in squares D1, E1 and F1 (red numbers).
In the small picture you can see the final solution for this part of the board. Within block K number 7 should be in square F3.
Sudoku Locked Candidate: Column - Block
Similarly, if in a column a candidate number is confined to a single block, it is ‘locked’ inside the block. Since the block can only have this number once, that candidate number can be removed from the other columns within that block.
Here you can see that within column C candidate number 1 only occurs inside block P (blue number in squares C8 and C9). So, within block P number 1 is ‘locked’ in column C. Therefore, candidate number 1 can be deleted in other columns within block P, i.e. in squares A9, B7 and B8 (red numbers). In the small picture you can see the final solution for this part of the board. Within block P number 1 should be in square C9.
Sudoku Locked Candidate: Block - Row
Conversely, if within a block a candidate number is confined to one row, it is 'locked' in that row. Since the number can occur only once in the row, that candidate number can be removed from that row outside the block.
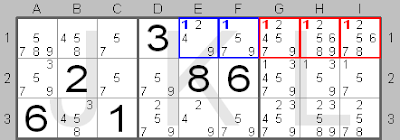
Here you can see that within block K candidate number 1 only occurs in row 1 (blue numbers in squares E1 and F1) - it is 'locked' in row 1. Therefore, outside block K candidate number 1 can be deleted in row 1, i.e. in squares G1, H1 and I1 (red numbers).
In the small picture you can see the final solution for this part of the board. Within block K number 1 should be in square E1.
Sudoku Locked Candidate: Block - Column
Similarly, if a candidate number in a block is confined to one column, it is 'locked' in that column. Since the number can occur only once in that column, that candidate number can be removed from the column outside the block.
Here you can see that within block P candidate number 7 only occurs in column A (blue number in squares A7 and A8) - it is 'locked' in column A. Therefore, in column A candidate number 7 can be deleted outside block P, i.e. in squares A4 and A5 (red numbers).
In the small picture you can see the final solution for this part of the board. Within block P number 7 should be in square A8.
By repeating finding ‘locked’ candidates in the sudoku puzzle, the number of candidates can be reduced considerably. Good luck!
Sudoku Locked Candidate: Row - Block
If in a row a candidate number is confined to a single block, it is 'locked' inside the block. Since the block can only have this number once, that candidate number can be removed from the other rows within that block.
Here you can see that within row 3 candidate number 7 only occurs inside block K (blue numbers in squares E3 and F3). So, within block K number 7 is ‘locked’ in row 3. Therefore candidate number 7 can be deleted in other rows within block K, i.e. in squares D1, E1 and F1 (red numbers). 
In the small picture you can see the final solution for this part of the board. Within block K number 7 should be in square F3. Sudoku Locked Candidate: Column - Block
Similarly, if in a column a candidate number is confined to a single block, it is ‘locked’ inside the block. Since the block can only have this number once, that candidate number can be removed from the other columns within that block.Here you can see that within column C candidate number 1 only occurs inside block P (blue number in squares C8 and C9). So, within block P number 1 is ‘locked’ in column C. Therefore, candidate number 1 can be deleted in other columns within block P, i.e. in squares A9, B7 and B8 (red numbers). In the small picture you can see the final solution for this part of the board. Within block P number 1 should be in square C9.
Sudoku Locked Candidate: Block - Row
Conversely, if within a block a candidate number is confined to one row, it is 'locked' in that row. Since the number can occur only once in the row, that candidate number can be removed from that row outside the block.
Here you can see that within block K candidate number 1 only occurs in row 1 (blue numbers in squares E1 and F1) - it is 'locked' in row 1. Therefore, outside block K candidate number 1 can be deleted in row 1, i.e. in squares G1, H1 and I1 (red numbers).
In the small picture you can see the final solution for this part of the board. Within block K number 1 should be in square E1.
Sudoku Locked Candidate: Block - Column
Similarly, if a candidate number in a block is confined to one column, it is 'locked' in that column. Since the number can occur only once in that column, that candidate number can be removed from the column outside the block.
Here you can see that within block P candidate number 7 only occurs in column A (blue number in squares A7 and A8) - it is 'locked' in column A. Therefore, in column A candidate number 7 can be deleted outside block P, i.e. in squares A4 and A5 (red numbers).
In the small picture you can see the final solution for this part of the board. Within block P number 7 should be in square A8.
By repeating finding ‘locked’ candidates in the sudoku puzzle, the number of candidates can be reduced considerably. Good luck!
Monday, October 26, 2009
What Makes A Good Sudoku Program?
A good sudoku program on your computer can greatly facilitate your sudoku game in many aspects. It can serve as a sudoku generator to make new sudoku puzzles of any degree of difficulty from beginner to very difficult. A good sudoku program can also make an unlimited number of new puzzles without repeating previous puzzles. The sudoku software should be intelligent enough to give you hints or clues during the solving process enabling you to reach the correct sudoku solution. So the sudoku program should in effect be both a sudoku generator and a sudoku solver. It should have a built-in sudoku algorithm, which should be able to solve even the most difficult sudoku puzzle. However, first and foremost it should be a friendly assistant helping you to solve the sudoku puzzle.
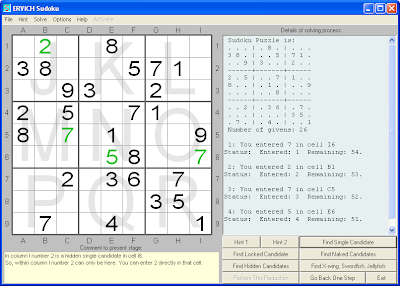
A great help in solving sudoku is to make a table (the candidate table) of possible candidate numbers, which may be placed in each of the empty squares at each stage. For example the number 2 cannot be placed in a square, if there is already a number 2 in the row, column or block in which the square is placed.
A good sudoku program can automati- cally calculate the candidate table and show it directly on the sudoku board in such way that you can see the possible numbers (the candidate numbers) for each of the empty squares. If a square has only one candidate (an obvious single candidate), then that number should be placed in the square. A single candidate may also be hidden among other candidates in a square (hidden single candidate).
When you find a square with a single candidate, then you can place that number in the square. Thereafter that candidate number needs to be removed from the candidate table for the three groups (row, column and block) of which the square is a part. A good sudoku program would do this automatically.
You can solve the easy sodoku puzzles just by finding single candidates. To solve the more difficult Sudoku puzzles, you need to reduce the number of candidates until single candidates appear. There are many methods for reducing candidates. Your sudoku program should be able to suggest candidate reduction according to a considerable number of methods. These include ’locked’ candidate, ‘naked’ candidates (pairs, triples, quads), ‘hidden’ candidates (pairs, triples, quads) and the more special x-wing, swordfish and Jellyfish.
Other features of a good sudoku program would include: easy entering of suduko puzzles from newspapers, books and magazines, saving and loading of puzzles, saving of sudoku puzzles in progress, a go back one step option, printing of sudoku puzzles, a timer option to record the time used to solve a given puzzle and a recording of the solving process.
A great help in solving sudoku is to make a table (the candidate table) of possible candidate numbers, which may be placed in each of the empty squares at each stage. For example the number 2 cannot be placed in a square, if there is already a number 2 in the row, column or block in which the square is placed.
A good sudoku program can automati- cally calculate the candidate table and show it directly on the sudoku board in such way that you can see the possible numbers (the candidate numbers) for each of the empty squares. If a square has only one candidate (an obvious single candidate), then that number should be placed in the square. A single candidate may also be hidden among other candidates in a square (hidden single candidate).When you find a square with a single candidate, then you can place that number in the square. Thereafter that candidate number needs to be removed from the candidate table for the three groups (row, column and block) of which the square is a part. A good sudoku program would do this automatically.
You can solve the easy sodoku puzzles just by finding single candidates. To solve the more difficult Sudoku puzzles, you need to reduce the number of candidates until single candidates appear. There are many methods for reducing candidates. Your sudoku program should be able to suggest candidate reduction according to a considerable number of methods. These include ’locked’ candidate, ‘naked’ candidates (pairs, triples, quads), ‘hidden’ candidates (pairs, triples, quads) and the more special x-wing, swordfish and Jellyfish.
Other features of a good sudoku program would include: easy entering of suduko puzzles from newspapers, books and magazines, saving and loading of puzzles, saving of sudoku puzzles in progress, a go back one step option, printing of sudoku puzzles, a timer option to record the time used to solve a given puzzle and a recording of the solving process.
Saturday, October 24, 2009
A Sudoku A Day Exercises The Brain
If there is one kind of addiction that is actually beneficial for adults and kids alike, it would be an addiction to sudoku puzzles. Researchers rank solving sudoku puzzles daily among the top ten non-traditional and alternative ways to boosts brain power. Other brain boosting moves include high-protein diets, listening to classical music, and lots of rest. These are simple but are rather difficult to follow because of budget limitations, personal preferences, and lifestyle. This is the advantage sudoku games holds over other brain boosters. They are accessible from newspapers, books, and even the Internet. They are also workable between breaks or at any spare time. So every time someone chastises you for doing sudoku again, kindly explain and hope that they pick up the habit too.
Though sudoku puzzles are not mathematical problems, solving the puzzles requires the most basic tool of mathematics and science: logic. Since the puzzles entail the use of logic, common sense, and concentration, the brain is put out of the stupor of doing routine, mundane tasks. In other words, your brain actually gets a break and a good work-out. Studies reveal that the more the brain uses its skills, the better it works. Brains that get more exercise are determined to be more active, and its cells are healthier. Researchers even associate sudoku brain exercises to physical exercise. They stress that just as physical exercise keeps muscle loss at bay, sudoku exercise keeps brain cells from dying and also encourages better brain function. Education is important, but studies actually show that students who do mental workouts like sudoku have higher IQs than students who do not. This only shows that doses of sudoku are more than just ways to pass time. They actually help in improving your ability to comprehend more complex ideas.
Ian Robertson, a neuroscientist, facilitated a research among the elderly with the premise that decreased mental ability is not inevitable with the right stimulation. The research included two groups of elderly people: the first group solved sudoku puzzles as part of their routine, while the second did not. After some time, their IQ levels were tested and compared to their test results before the experiment. The sudoku-solving group was found to have increased their mental abilities by a significant percentage while the other group showed no change. Dr. Robertson cited a similar research wherein 3,000 people, aged 65-94, were found to have increased their mental capabilities and age by as much as 14 years, just by ten sessions of brain boosting exercise like sudoku.
Other experts agree with these findings, saying that solving challenging mind games like sudoku puzzles inhibit or prevent the development of memory loss. Health trends also show that adults with demanding, and intellectually challenging jobs benefit from better mental function when they age. Sudoku functions just like these jobs because it requires brain exertions.
As it is, experts advise adults to encourage children to solve puzzles like sudoku to start mental improvement earlier in life. Sudoku exercises are actually adopted by some schools to stimulate thinking and foster better academic performance of their students. So instead of letting kids watch TV, or read comics, hand them sudoku puzzles. Then, both you and your kids can defend your love of sudoku to those poor souls who do not understand the beauty, joy, and benefits of solving sudoku.
For more valuable information on sudoku puzzles please visit http://www.sudoku-puzzles.com
Article Source: http://EzineArticles.com/?expert=Earl_Talbot
Though sudoku puzzles are not mathematical problems, solving the puzzles requires the most basic tool of mathematics and science: logic. Since the puzzles entail the use of logic, common sense, and concentration, the brain is put out of the stupor of doing routine, mundane tasks. In other words, your brain actually gets a break and a good work-out. Studies reveal that the more the brain uses its skills, the better it works. Brains that get more exercise are determined to be more active, and its cells are healthier. Researchers even associate sudoku brain exercises to physical exercise. They stress that just as physical exercise keeps muscle loss at bay, sudoku exercise keeps brain cells from dying and also encourages better brain function. Education is important, but studies actually show that students who do mental workouts like sudoku have higher IQs than students who do not. This only shows that doses of sudoku are more than just ways to pass time. They actually help in improving your ability to comprehend more complex ideas.
Ian Robertson, a neuroscientist, facilitated a research among the elderly with the premise that decreased mental ability is not inevitable with the right stimulation. The research included two groups of elderly people: the first group solved sudoku puzzles as part of their routine, while the second did not. After some time, their IQ levels were tested and compared to their test results before the experiment. The sudoku-solving group was found to have increased their mental abilities by a significant percentage while the other group showed no change. Dr. Robertson cited a similar research wherein 3,000 people, aged 65-94, were found to have increased their mental capabilities and age by as much as 14 years, just by ten sessions of brain boosting exercise like sudoku.
Other experts agree with these findings, saying that solving challenging mind games like sudoku puzzles inhibit or prevent the development of memory loss. Health trends also show that adults with demanding, and intellectually challenging jobs benefit from better mental function when they age. Sudoku functions just like these jobs because it requires brain exertions.
As it is, experts advise adults to encourage children to solve puzzles like sudoku to start mental improvement earlier in life. Sudoku exercises are actually adopted by some schools to stimulate thinking and foster better academic performance of their students. So instead of letting kids watch TV, or read comics, hand them sudoku puzzles. Then, both you and your kids can defend your love of sudoku to those poor souls who do not understand the beauty, joy, and benefits of solving sudoku.
For more valuable information on sudoku puzzles please visit http://www.sudoku-puzzles.com
Article Source: http://EzineArticles.com/?expert=Earl_Talbot
Boost Your Child's Brainpower with Sudoku
In less than a year the Sudoku bug has infected huge numbers of the UK population, and it is fast spreading across the world! Why has a simple logic puzzle become so popular, and how can your kids benefit?
Sudoku puzzles were first published in the US in the 1970s and are sometimes known as "Number Squares". They have been popular for many years in Japan, where the name "Sudoku" (meaning "single number") was coined. The current craze was started late in 2004 when a UK newspaper started publishing the puzzles. Within weeks the puzzles were picked up in other newspapers and Sudoku became the pastime of choice for commuters, parents – and even kids!
From a parent’s point of view, Sudoku puzzles are perfect for long journeys, waiting rooms, and rainy afternoons. They are being found more and more in the classroom as teachers wake up to their benefits and use them as time-fillers for children who finish early, as whole class activity, or as "homework". Indeed, the UK government-produced Teachers magazine has recommended that Sudoku puzzles are used in the classroom as brain exercise!
As well as developing your child's logic and reasoning skills and concentration, Sudoku puzzles, if done at the right level, build your child's confidence. Children of all abilities enjoy the challenge of a Sudoku puzzle, if the puzzle is age-appropriate. Bear in mind that many of the puzzles published in newspapers are too difficult for younger children, so it is worth seeking out puzzles made especially for kids. Children as young as five years old can try the 4x4 grids, then build up to the 6x6 grids and finally the traditional 9x9 sudoku grid.
Why are Sudoku so appealing? Firstly, although Sudoku grids usually use numbers, your child does not need mathematical skills to solve the puzzles – only logic. Using logical reasoning appropriate to his/her age, your child decides how to place numbers into a Sudoku grid. There is only one correct answer for each puzzle, no guessing is necessary, and the rules are easy to learn. The more puzzles you do, the better you become. Each puzzle typically takes a child about 20-30 minutes to complete, and gives them a real sense of satisfaction when finished!
And that, really, is the secret of their popularity. You feel good when you finish one! And then you want to try another one, and another ….
Lindsay Small is the owner of Activity Village, packed full of fun and educational activities for kids. Do you have children aged 2-10? Visit http://www.ActivityVillage.co.uk to find free kids crafts, printables, educational resources, worksheets, coloring pages and puzzles, jigsaws and, of course, Sudoku puzzles!
Article Source: http://EzineArticles.com/?expert=Lindsay_Small
Sudoku puzzles were first published in the US in the 1970s and are sometimes known as "Number Squares". They have been popular for many years in Japan, where the name "Sudoku" (meaning "single number") was coined. The current craze was started late in 2004 when a UK newspaper started publishing the puzzles. Within weeks the puzzles were picked up in other newspapers and Sudoku became the pastime of choice for commuters, parents – and even kids!
From a parent’s point of view, Sudoku puzzles are perfect for long journeys, waiting rooms, and rainy afternoons. They are being found more and more in the classroom as teachers wake up to their benefits and use them as time-fillers for children who finish early, as whole class activity, or as "homework". Indeed, the UK government-produced Teachers magazine has recommended that Sudoku puzzles are used in the classroom as brain exercise!
As well as developing your child's logic and reasoning skills and concentration, Sudoku puzzles, if done at the right level, build your child's confidence. Children of all abilities enjoy the challenge of a Sudoku puzzle, if the puzzle is age-appropriate. Bear in mind that many of the puzzles published in newspapers are too difficult for younger children, so it is worth seeking out puzzles made especially for kids. Children as young as five years old can try the 4x4 grids, then build up to the 6x6 grids and finally the traditional 9x9 sudoku grid.
Why are Sudoku so appealing? Firstly, although Sudoku grids usually use numbers, your child does not need mathematical skills to solve the puzzles – only logic. Using logical reasoning appropriate to his/her age, your child decides how to place numbers into a Sudoku grid. There is only one correct answer for each puzzle, no guessing is necessary, and the rules are easy to learn. The more puzzles you do, the better you become. Each puzzle typically takes a child about 20-30 minutes to complete, and gives them a real sense of satisfaction when finished!
And that, really, is the secret of their popularity. You feel good when you finish one! And then you want to try another one, and another ….
Lindsay Small is the owner of Activity Village, packed full of fun and educational activities for kids. Do you have children aged 2-10? Visit http://www.ActivityVillage.co.uk to find free kids crafts, printables, educational resources, worksheets, coloring pages and puzzles, jigsaws and, of course, Sudoku puzzles!
Article Source: http://EzineArticles.com/?expert=Lindsay_Small
Sudoku – the truly international game
The immensely popular game Sudoku is based on placing nine different signs - usually the numbers 1 to 9 - on a square board with 81 squares. The board has 9 rows, 9 columns and 9 blocks of 3 x 3 squares. Within each group of squares – row, column and block - the 9 different signs must only occur once.
The game only requires the nine different signs to be placed on the board according to simple logic. You need no special qualification and no knowledge of any specific language. Sudoku is for everyone irrespective of nationality, gender, age, religion, occupation or any other characteristic you may think of. So it is a truly international, cross-cultural game. You can play it at home, during travel, on vacation - almost anywhere - except perhaps when your absorption in the game would be inconvenient to your fellow companion!
At the beginning of the game some of the squares hold a number (the given numbers or clues). Your job is to fill the empty squares with numbers, which have not yet been used, so that each row, column and block in the end will hold all the numbers from 1 to 9. Thus each square contributes to or is a part of three groups: a row, a column and a block. In each of the groups the numbers from 1 to 9 should be placed.
A Sudoku puzzle is solved by logic - applying the method of elimination. You rule out all numbers, which cannot be placed in a given square, until only one number is left. That number should then be placed in the square. Guessing would inevitably lead to errors, which may be difficult to correct. The challenge of the game is to assess effectively the possible placement of numbers in the squares.
You can find Sudoku puzzles in newspapers, magazines and books. On the Internet you can also find Sudoku puzzles as well as computer programs, which can design and solve Sudoku puzzles.
A fine sudoku program can be found here.
Sudoku puzzles can be made with any degree of difficulty, so there would be challenging puzzles for anyone to solve, from the beginner to the extremely skilled. The easy puzzles generally have a large number of given numbers or clues (30 or more). The most difficult, which can be extremely difficult to solve, would generally have a lesser number of clues (down to 17).
Sudoku puzzles stimulate your brain and keep you mentally fit as long as you live. So there is every reason for you to go Sudoku!
The game only requires the nine different signs to be placed on the board according to simple logic. You need no special qualification and no knowledge of any specific language. Sudoku is for everyone irrespective of nationality, gender, age, religion, occupation or any other characteristic you may think of. So it is a truly international, cross-cultural game. You can play it at home, during travel, on vacation - almost anywhere - except perhaps when your absorption in the game would be inconvenient to your fellow companion! At the beginning of the game some of the squares hold a number (the given numbers or clues). Your job is to fill the empty squares with numbers, which have not yet been used, so that each row, column and block in the end will hold all the numbers from 1 to 9. Thus each square contributes to or is a part of three groups: a row, a column and a block. In each of the groups the numbers from 1 to 9 should be placed.
A Sudoku puzzle is solved by logic - applying the method of elimination. You rule out all numbers, which cannot be placed in a given square, until only one number is left. That number should then be placed in the square. Guessing would inevitably lead to errors, which may be difficult to correct. The challenge of the game is to assess effectively the possible placement of numbers in the squares.
You can find Sudoku puzzles in newspapers, magazines and books. On the Internet you can also find Sudoku puzzles as well as computer programs, which can design and solve Sudoku puzzles.
A fine sudoku program can be found here.
Sudoku puzzles can be made with any degree of difficulty, so there would be challenging puzzles for anyone to solve, from the beginner to the extremely skilled. The easy puzzles generally have a large number of given numbers or clues (30 or more). The most difficult, which can be extremely difficult to solve, would generally have a lesser number of clues (down to 17).
Sudoku puzzles stimulate your brain and keep you mentally fit as long as you live. So there is every reason for you to go Sudoku!
Subscribe to:
Posts (Atom)
